
Os enigmas mais intrigantes
São aparentemente simples, mas os antigos não conseguiram resolverFoto: Bearfotos

Cilada matemática
A Antiguidade lidou com problemas matemáticos aparentemente simples, mas impossíveis de resolver até os avanços em geometria analítica, álgebra, cálculo e teoria dos números.Foto: Wikimedia Commons
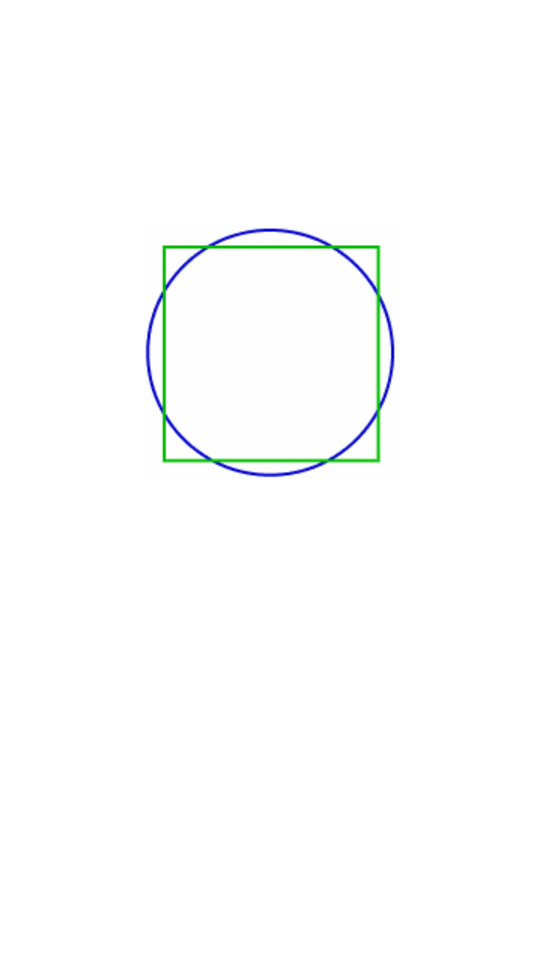
Quadratura do Círculo
Um deles era transformar um círculo em um quadrado com a mesma área, usando apenas régua e compasso. Parece factível, mas esconde uma complexidade.Foto: Wikimedia Commons

O π da questão
Este problema persistiu até entendermos profundamente o número π, revelando que, como o π não pode ser representado como a maioria dos números comuns, o desafio era impossível com o conhecimento da época.Foto: Reprodução
Trissecção do Ângulo
Outra treta para os antigos: dividir qualquer ângulo em três partes iguais com simples régua e compasso.Compasso, compasso meu...
A solução geral fugia das possibilidades daquela época. Com um compasso, ferramenta básica, conseguimos dividir um ângulo em dois. Agora, em três... nada feito.Foto: Wikimedia Commons
Polígonos Regulares
Dividir um círculo em partes iguais para criar polígonos regulares com ferramentas básicas era outro desafio. Como fazer isso com polígonos de 17 lados? Mistério.Meu nome é Gauss 🎶 🎶
Quem mais avançou nisso foi o matemático Karl Friedrich Gauss, mas ele só conseguiu uma solução parcial para o problema. A resposta definitiva teve que esperar por avanços na matemática.Foto: Wikimedia Commons
Antes de ir...
Você sabia que a pirâmide mais antiga do mundo pode estar "escondida" fora do Egito?Foto: Osama Elsayed/Unsplash
Curtiu?
Siga o Byte para ficar por dentro dos melhores conteúdos sobre ciência e tecnologia.Foto: Unsplash